Instruments of Critical Path
By Michael J. Scianamblo, DDS
Abstract
Instruments of Critical Path are a new set of endodontic instruments used to clean and enlarge the root canal space. Various prototypes that have been provided by Maiffeler (Dentsply International) are referred to nominally as X‐Files or Swaggering Files. The instruments feature symmetrical cross‐sections that are off‐set, placing the center of mass of the instrument at a specified distance away from the axis of rotation. The off‐set center of mass allows the instruments to generate precession, and form mechanical waves within the canal. Part I discusses the “critical path” of the root canal space, which is defined as a path that is equidistant circumferentially from the center of the canal forming an ideal endodontic cavity preparation. A theoretical or “critical set” of instruments is described, whereby the diameter of the files increase equally and is a function of the area of a circleπr^2, thereby expanding exponentially.
Introduction
The objective of a root canal preparation or ECP (endodontic cavity preparation) is to create a space that can be predictably cleaned or disinfected and filled to prevent further infection. These objectives were outlined by the earliest investigators Hunter (1911), Hess (1916), Rosenow (1917) and Stewart (1955). The first endodontic instruments were introduced by Maynard in 1838, who fashioned them from notched piano wire. They were called rat‐tail or R‐Type files and are still in use as the barbed broaches (Figure 1A). The Kerr Manufacturing Company developed K‐Type instruments (Kerr, 1919). Examples of K‐Type instruments are reamers and files (Fig 1B and C). They are available in carbon steel, stainless steel, and more recently, an alloy of nickel‐titanium. Traditional files and reamers were manufactured in 21, 25 and 30 mm lengths with a working or cutting surface that was extending from the tip (D0) to shank (D16) with a standardized 0.02mm per mm taper (see figure 2). H‐‐type files are manufactured by grin ding flutes into tapered round metal blank s to form a series of intersecting cones. During use, cutting occurs in the pull direction only. Hedstrom files (Fig. 1DD) are extremely efficient cutting instruments due primary to the fact that they have positive cutting angles.
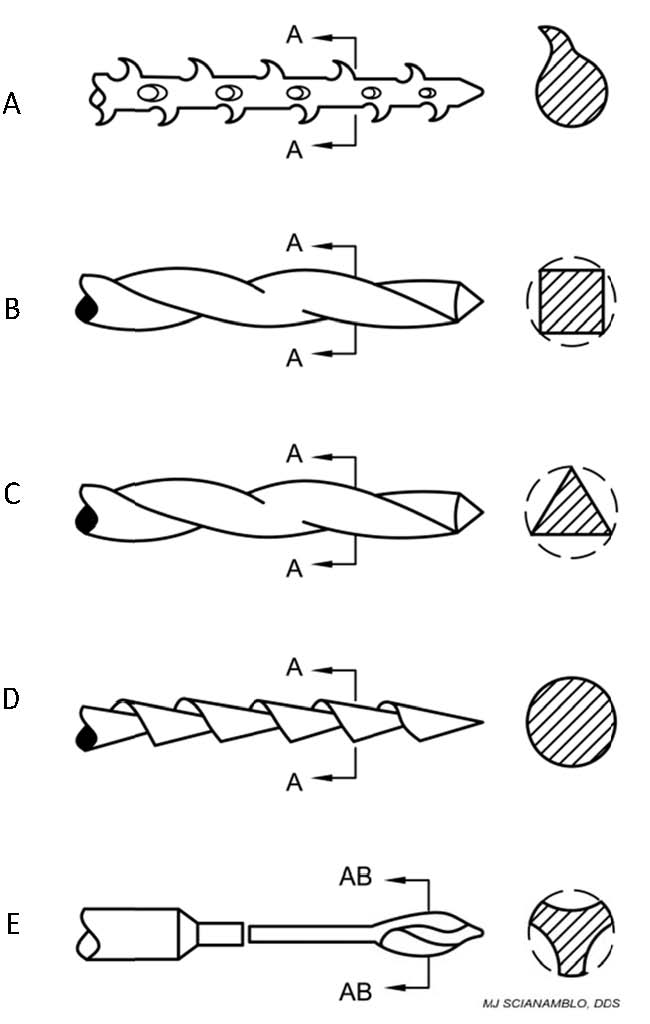
Figure 1
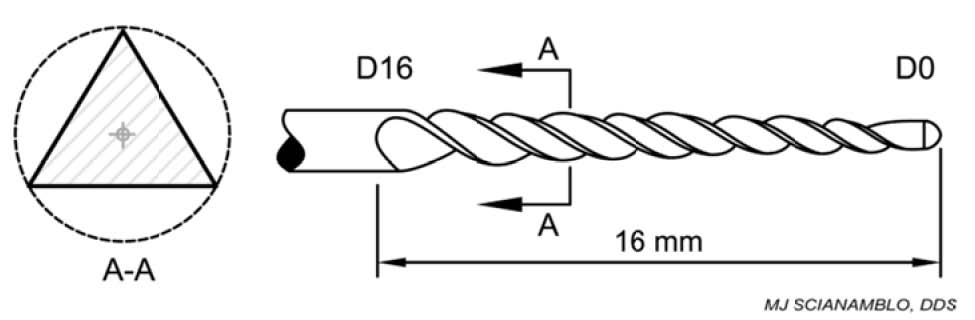
Figure 2Schilder ( 1974) was the first clinician to provide a detailed discussion off the root canal preparation referring to the procedure as cleaning and shaping and outlined specific design objectives, which included thee continuously tapering shape. This tapering space was acquired by hand instrumentation alternating reamers and files creating an “envelope of motion”. Weine et al (1975) used clear acrylic blocks to evaluate the effectiveness of various instrumentation techniques. Their conclusions were somewhat disconcerting, demonstrated that the utilization of standard instruments in either a reaming, filing, or a reaming and filing produced preparations that were irregular i n shape and not continuously tape ring. The narrowest part, the so called “elbow”, was located at a point coronal to the root apex. These characteristics were felt to result from the elastic memory off instruments and a predilection to straighten as they are migrated around curves. Too alleviate this problem, Weine suggested removing the flutes from the outer surface of a pre‐curved file, and thee use of instruments in intermediate ISO (International Standards Organization)) sizes by cutting a small segment from thee tip of the instrument. Coffae and Brilliant (1976) corroborated the work of Schilder demonstrating that a tapering preparation was more efficacious in the removal of debris from the confines of the root canal system than parallel preparations. They also demonstrated that the use of files serially , and in a step‐back modality, was more effective in producing the tapering shape. Too minimize the problems described by Weine, Abou Rass et al (1980) engaged in a discussion of anti‐curvature filing.
This method advocated the removal of conspicuous amounts of tooth structure from the outer walls of the curve of a root canal system. This provided a safer approach to the root apex, in addition to protecting the furcation of multi‐rooted teeth. Marshall and Pappin (1980) advocated an innovative approach to root canal preparation described as a crown‐down technique. This method addresses the canal by expanding the preparation coronally before an attempt is made to reach the apex. Pre‐curvature of instruments was found to be unnecessary, however, the apical zip, as described by Weine, could still be detected. Roane et al (1985), described a technique for root canal preparation called “balanced force”. The technique was a variation of reaming, which included “back‐turning” the file in a counter‐clockwise direction, and purportedly maintained the contour of the canal without transporting the apical foramen. Theoretically, the restoring force or elastic memory of the file, as described by Weine, was be overcome when it is pit against dentinal resistance. However, Blum, Machtou and others (1997) found that these techniques, were a predisposing factors associated with unpredictable breakage. The advent of Nickel‐Titanium rotary instrumentation has changed the landscape of endodontic cavity preparation measurably. The earliest investigators including Glosson et al (1995) and Esposito et al (1995), suggested that Nickel‐Titanium rotary instruments were superior to hand instrumentation in maintaining the original anatomy requiring fewer instruments. However, Schafer (1999) found that Nickel‐Titanium instruments with traditional cross‐sections and sizes left all curved canals poorly cleaned and shaped, whereby tooth structure was removed almost exclusively from the outer‐wall of the curve. Kum et al (2000), Calberson et al (2002), and Schafer and Florek (2003) stated that the greatest failing of current NiTi designs is the continued predisposition to torsional and cyclic fatigue and breakage. Current research does not completely endorse hand instrumentation or rotary instrumentation exclusively. Endodontic cavity preparations, however, will be done using booth hand instruments and rotary instruments due too the facility and safety of these instruments, when used in combination. In addition, rotary instrumentation facilitates thee coronal removal of debris, which is desirable.
The Endodontic File Sequence
The challenges of current Nickel Titanium instrument designs, as described above, may be compounded by the problems associated with the instrument sequence itself. Specifically, instruments that increase in size too rapidly can be subjected to rapid increases in the work load, which predisposes the instrument to inefficiency, premature fatigue and breakage. The resistance that an instrument encounters increases exponentially as the size or diameter of the instrument increases. As the canal is enlarged, changes occur in the circumference or perimeter of the ECS and the area that is being enlarged. These changes can be calculated using the formulas for the circumference of a circle C = 2pr, the area or a circle A = pr2, and the lateral surface area of a truncated cone, also known as a frustum, Sf = ps (r1 + r2).
To further evaluate the enlargement of the ECS (endodontic cavity space) or root canal space, we need to examine a theoretical tooth model and ideal root canal preparation (Figures 3A and 3B).

FIG. 3A and FIG. 3BA prepared ECS (endodontic cavity space) is shown in Figure 3B. Although disagreements may exist regarding the configuration of an ideal endodontic cavity preparation, described here as the ECP, or root canal preparation, it is generally agreed that the preparation should be small in the apical foramen (from 0.20-0.30mm) and large in the orifice (from 1.0 –1.2 mm). If we calculate the change in surface areas of the ECP, between the orifice and the foramen as the space is enlarged circumferentially (and equally), we can better estimate the changes in resistance that an instrument undergoes. Referring to figure 4B, if the prepared canal between the orifice and the foramen were assumed to be 12mms in length (the average length of that space) and that length was sectioned transversely into twelve equal segments, each segment could be viewed separately. These segments are called frustums with the diameter continually increasing from the foramen to the orifice. These frustums are nominally referred to as D0 – D12.

FIG. 4A, FIG. 4B and FIG. 4CReferring back to figure 3A, assuming that the diameter of the ECS averages 0.20mm (initially) along its entire length, the surface area of each of a transverse cross-section of any part of the original canal would equal pr2 or A = p times (0.10)2, which equals 0.0314 mm2. Referring to figure 4A and 4B, if the diameter of the foramen (D zero) would remain at 0.20mm and the diameter at the orifice (D12) would increase nominally 1.0mms, the diameter at the orifice would equal 1.2mm and the middle diameter (D6) would equal to 0.70mm. The outline of this ideal cavity preparation in (figure 3B) is termed the “critical path” of the endodontic cavity preparation. In calculating the increases in surface areas of the various cross-sections as the canal is enlarged and using the formula for the area of a circle A = pr2, the area at the orifice at D12 would increases from 0.0314 mm2 to 1.1131 mm2. This is an increase in size of approximately 36 times. If the same calculation were made at D6, the diameter of the ECS would increase from 0.0314 mm2 to 0.7854 mm2 and increase in size of 25 times. Thus, each of these areas is seen to increase exponentially not linearly or geometrically. Almost all manufactures of endodontics instruments use the ISO system to sequence files, which is linear (see table 1). Thus, arriving at an ideal ECP efficiently and safely with a small number of instruments is problematic useless an exponential system for sizes is adopted.
The cross-sectional diameters of traditional instruments specified by the ISO System. Instruments or tip sizes 20-70 with an invariable taper 0.02mm per mm are shown.
Expressed in 100’s of mm’s
| 20/02 | 25/02 | 30/02 | 35/02 | 40/02 | 45/02 | 50/02 | 55/02 | 60/02 | |
| D1 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| D2 | 22 | 27 | 32 | 37 | 42 | 47 | 52 | 57 | 62 |
| D3 | 24 | 29 | 34 | 39 | 44 | 49 | 54 | 59 | 64 |
| D4 | 26 | 31 | 36 | 41 | 46 | 51 | 56 | 61 | 66 |
| D5 | 28 | 33 | 38 | 43 | 48 | 53 | 58 | 63 | 68 |
| D6 | 30 0% |
35 17%* |
40 14% |
45 13% |
50 11% |
55 10% |
60 9% |
65 8% |
70 7% |
| D7 | 32 | 37 | 42 | 47 | 52 | 57 | 62 | 67 | 72 |
| D8 | 34 | 39 | 44 | 49 | 54 | 59 | 64 | 69 | 74 |
| D9 | 36 | 41 | 46 | 51 | 56 | 61 | 66 | 71 | 76 |
| D10 | 38 | 43 | 48 | 53 | 58 | 63 | 68 | 73 | 78 |
| D11 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 |
| D12 | 42 | 47 | 52 | 57 | 62 | 67 | 72 | 77 | 82 |
*Represents the percentage increase in areal diameter from the previous cross-sectional. The average of these changes from at D6 is 10%.
Table 1
Further evaluating the conventional ISO system, we again refer to figure 2 and the diameter at D1. The instruments are specified to increase in 0.05mm increments from as D1 beginning with the number 10, which is 0.10mm at D1, progressing to the number 15, which is 0.15mm, and continuing 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50, 0.55, up to 0.60. Then, the instruments increase in size via 0.10mm increments to 0.70, 0.80, 0.90, 1.00 etc. All instruments maintain a constant taper of 0.02mm per mm (with calibrations in 100ths of mms) from D1 to D16. Thus, using an ISO sequence of instruments to increase the diameter at D6 from 0.20mm to 0.70mm would require the use of at least 9 different instruments that increase in diameter linearly and somewhat randomly. As seen in table 1, the change in diameter from a size 30 file to a size 70 file at D6 ranges from 17% to 8%. Thus, the change in diameter over this 9 instrument sequence is exactly 9% or a linear change of exactly 1% per instrument. While it may be reasonably safe it is not considered efficient, and is inconsistent with the rapid change in diameter that occurs during ECP.
Other investigators have recognized the deficiencies of the ISO system. Schilder (1991) attempted to mitigate the problem by imposing a constant 29.17% increase size of the diameter of the instrument at D1, while maintaining a constant taper of 0.02mm/mm. This instrument set was called Series 29, whereby the ISO #10 (0.10mm at D1) was designated as the No. 1 and the ISO #60 (0.60mm at D1) the No.8. As described in the patent, literature this system could also be applied to a set of 6 instruments with a constant 43.1% increase at D1 or a set of 7 instruments with a constant 34.8% increase at D1. Although Schilder did not delineate this mathematical formula to determine how a set containing N number of instruments would have an equal percent increase, you would need N-1 steps to get from instrument no. 1 (0.10mm at D1) to the number 8 (0.60mm at D1). You would then need to find the increase ratio, A, where A=6^(1/N-1). For a series of 8 instruments A = 6^(1/(8-1) or 6^(1/7). To find percent, we multiply the ratio by 100%, and then to find increase, we subtract 100%. A numerical sequence whereby each term (or number) is multiplied by the same factor to obtain the following term is a called geometric sequence. Thus, this set of instruments was more efficient, but was geometrical not exponential, which is more logical.
With the introduction of nickel-titanium alloys in endodontic drill manufacture, it became clear that large amounts of tooth structure could be removed rapidly in and around the greater curvature of the canal. This inspired the introduction of a broad range of new instruments with common tip sizes, but with tapers that were significantly greater than the 0.02 taper of the ISO conventional instruments (McSpadden 1998 and Johnson, 2000). These included instruments with 0.04, 0.6, 0.8, 1.0 and 1.2 mm per mm tapers. Some of the first nickel-titanium instruments to become popular were Profile and the Profile GT manufactured by Tulsa Dental Products. The distribution of the diameters of the 0.06 tapered instruments is listed in table 2 below. Although fewer instruments are required to carry out the same work as the instruments designated by the ISO system, it can be seen that these instruments still increase in size linearly. With these deficiencies in mind, a new instrument sequence derived by subdividing the ECP, and particularly the most vulnerable area of the canal, into equal parts was undertaken. This set of instruments is termed the “critical set” which dictates equal subdivision of the “critical path” (see Figure 5A and 5B).
The arrays of diameters using tip sizes 15, 20, 25, 30, 35, and 40 and 0.06 tapers of typical NiTi instruments are shown below.
Expressed in 100’s of mm’s
|
15/06 |
20/06 |
25/06 |
30/06 |
35/06 |
40/06 |
|
| D1 |
15 |
20 |
25 |
30 |
35 |
40 |
| D2 |
21 |
26 |
31 |
36 |
41 |
46 |
| D3 |
27 |
32 |
37 |
42 |
47 |
52 |
| D4 |
33 |
38 |
43 |
48 |
53 |
58 |
| D5 |
39 |
44 |
49 |
54 |
59 |
64 |
| D6 |
45 |
50 |
55 |
60 |
65 |
70 |
| D7 |
51 |
56 |
61 |
66 |
71 |
76 |
| D8 |
57 |
62 |
67 |
74 |
77 |
82 |
| D9 |
63 |
68 |
73 |
80 |
83 |
88 |
| D10 |
69 |
74 |
79 |
86 |
89 |
94 |
*Represents the percentage increase in areal diameter from the previous cross-sectional. The average of these changes from at D6 is 7.5%.
Table 2
Instruments of Critical Path-Progressive and Equal Diameters Method
Again, referring to Figure 4A, 4B and 4C, the critical path of the endodontic cavity preparation has been defined as that space which lies between the orifice area and the foramen of the tooth, whereby the diameter of the canal has been enlarged from of the foramen to the orifice and approximates 0.20mms to 1.2mms respectively and has a continuously tapering shape. Experienced clinicians are aware, that the instruments used in this enlargement procedure, particularly nickel-titanium rotary instruments, are most vulnerable at the fulcrum or greatest curvature of the critical path. Indeed, instrument failure is rare in canals that are reasonably straight. Although the point of greatest curvature is somewhat variable, it is clear that the point, also known as the elbow of the curve, is most often equidistant between D0 and D12 or the mid-point of the preparation. If the average length of the critical path is 12mm, the fulcrum would most often be found at D6 or that segment located approximately 6mm from the foramen. Thus, if six separate instruments are employed to accomplish the work of enlarging a curved canal, an ideal sequence of instruments could be constructed by calculating the changes that occur in the diameter of the ECS at D6 or the elbow of the curve. More specifically, if the canal is to be enlarged sequentially from 0.20 to 0.70mm at D6 and 0.20 to 1.2 mm at D12, an instrument set where the diameter of each instruments increases in area equally can be devised using the formula of the area of a circle A = pr2.
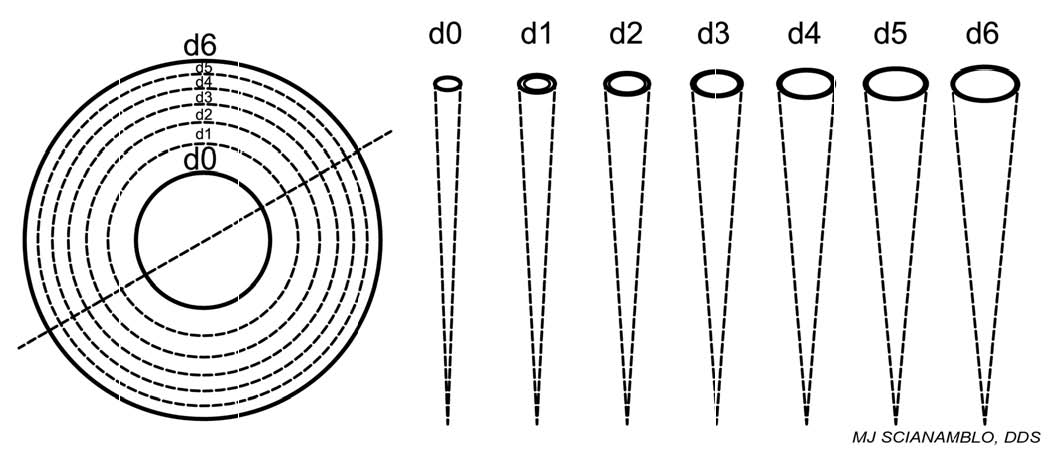
The specific calculations for these values can be found in table 3 and are derived in the following manner. With reference to D6 of Figure 4C and referring to Figures 5A and 5B , an outer circle and an inner circle form an annulus. If the total area of the inner circle is subtracted from the total area if the outer circle, the total area to be prepared or enlarged can be defined. Thus, the total area of the annulus at D6 can be subdivided into six separate areas each with its own diameter. These diameters may be nominally referred to as d0, d1, d2, d3, d4, d5, and d6 with corresponding radii r0, r1, r2, r3, r4, r5, and r6.
A outer circle – A inner circle = p (.35)2 – p(.1)2
A of annulus at D6 = p(.1225)- p(.01)
A of annulus at D6 = p(.1125)
If the annulus were then divided equally into 6 segments to fashion an ideal or model set of instruments, also called the “critical set”, then each instrument would increase in diameter by one-sixth the total area of the annulus at D6 or
A of annulus at D6/6 = p(.1125)/6= p 0.01875
Thus, a formula to determine the various radii that emerge at D6 as the area of annuli at D6 are divided equally, whereas n is the number of the annuli to be prepared, is
prn2 = prn-1 2 + p 0.01875
= rn2 = rn-1 2 + 0.01875
= rn2 = rn-1 2 + 0.01875
Thus, the radius that occurs at r1 after instrument No. 1 is allowed to prepare the canal to its maximum diameter is
r12= ro2 + 0.01875
r12= (0.1)2 + 0.01875
r12= 0.010 + 0.01875
r12= 0.0388
r1= 0.1696
If the diameter is twice the radius, then the inner diameter of D6 is d1, which is d1= 0.339mm.
Continuing to use the formula = rn2 = rn-1 2 + 0.01875, values for r2, r3, r4, r5, and r6 can be determined and in term values for d2, d3, d4, d5, and d6 at D6 whereby the critical set of instrument can be derived.
The cross-sectional diameters, d1, d2, d3, d4, d5, and d6, that occur at D0, D6, and D12 in the critical path of an endodontic cavity preparation. These diameters can be utilized to develop an ideal or preferred set of instruments, also called the critical set, and is, for the moment, theoretical.
Result
The total area of annulus at D6 can be subdivided into six separate areas each with its own diameter. These diameters may be nominally referred to as d1, d2, d3, d4, d5, and d6
| d0 | d1 | d2 | d3 | d4 | d5 | d6 | |
| D0 | .20 | .20 | .20 | .20 | .20 | .20 | .20 |
| D6 | .20 | .339 70%* |
.436 28% |
.515 15% |
.583 13% |
.644 10% |
.700 8% |
| D12 | .20 | .522 | .712 | .86 | .986 | 1.098 | 1.2 |
*Represents the percentage increase in cross-sectional area from the previous diameter or instrument.
Table 3
As mentioned above, constructing the critical instrument set will necessarily require tip sizes and tapers that cannot be garnered from conventional endodontic instruments classified by the ISO system, which vary linearly. A distributions of instrument diameters that would correspond to the critical path concept using novel tip sizes and tapers is offered below (see table 4). Interestingly, the average increase in diameter is 29%, however, this increase is achieved via an exponential progression not a geometric progression as described by Schilder (1991).
Examples of arrays of diameters of instruments which conform to the “critical path” could be expressed as follows:
Expressed in 100’s of mm’s
|
20/00 |
15/05 |
20/06 |
24/07 |
27/08 |
29/09 |
30/10 |
|
|
D1 |
20 |
15 |
20 |
24 |
27 |
29 |
30 |
|
D2 |
20 |
20 |
26 |
31 |
35 |
38 |
40 |
|
D3 |
20 |
25 |
32 |
38 |
43 |
47 |
50 |
|
D4 |
20 |
30 |
38 |
45 |
51 |
56 |
60 |
|
D5 |
20 |
35 |
44 |
52 |
59 |
65 |
70 |
|
D6 |
20 |
40 |
50 |
59 |
67 |
74 |
80 |
| Critical Set |
20 |
.339 |
.436 |
.515 |
.583 |
.644 |
.700 |
|
D7 |
20 |
45 |
56 |
66 |
75 |
81 |
90 |
|
D8 |
20 |
50 |
62 |
73 |
83 |
90 |
100 |
|
D9 |
20 |
55 |
68 |
80 |
91 |
99 |
110 |
|
D10 |
20 |
60 |
74 |
87 |
99 |
108 |
120 |
|
D11 |
20 |
65 |
80 |
94 |
107 |
117 |
130 |
|
D12 |
20 |
70 |
86 |
101 |
115 |
126 |
140 |
Table 4
Discussion
Providing a set of instruments that corresponds to the critical path concept, but has tip sizes and tapers that are recognizable to most clinician is challenging. The tip sizes and tapers provided by a novel set of instruments termed ProTaper Next, manufactured by Maillefer dental products accomplishes this objective (see table 5).
An array of five instruments in accordance with the “critical path” concept with common tips sizes and tapers
Expressed in 100’s of mm’s
|
20/00 |
17/04 | 25/06 | 30/07 | 40/06 | 50/06 | |
| D1 |
20 |
17 | 25 | 30 | 40 | 50 |
| D2 |
20 |
21 | 31 | 37 | 46 | 56 |
| D3 |
20 |
25 | 37 | 44 | 52 | 62 |
| D4 |
20 |
29 | 43 | 51 | 58 | 68 |
| D5 |
20 |
33 | 49 | 58 | 64 | 68 |
| D6 |
20 |
37 85% |
55 32% |
65 15% |
70 7% |
75 6% |
| Critical Set | .339 70%* |
.436 28% |
.515 15% |
.583 13% |
.644 10% |
Table 5
It can be further modified by applying variable tapers as defined by Maillefer (1998). When the volumetric expansion of the root canal space is calibrated by measuring the diameter of the X-files and plotted from D0 (apex) to D10 (foramen), substantial uniformity in dentin removal is possible (figure 6). The X-1 is the only instrument that deviates slightly from this uniformity, but may still be considered safe, because it would have the narrowest cross-section at D6, and therefore be the most flexible instrument in the set.
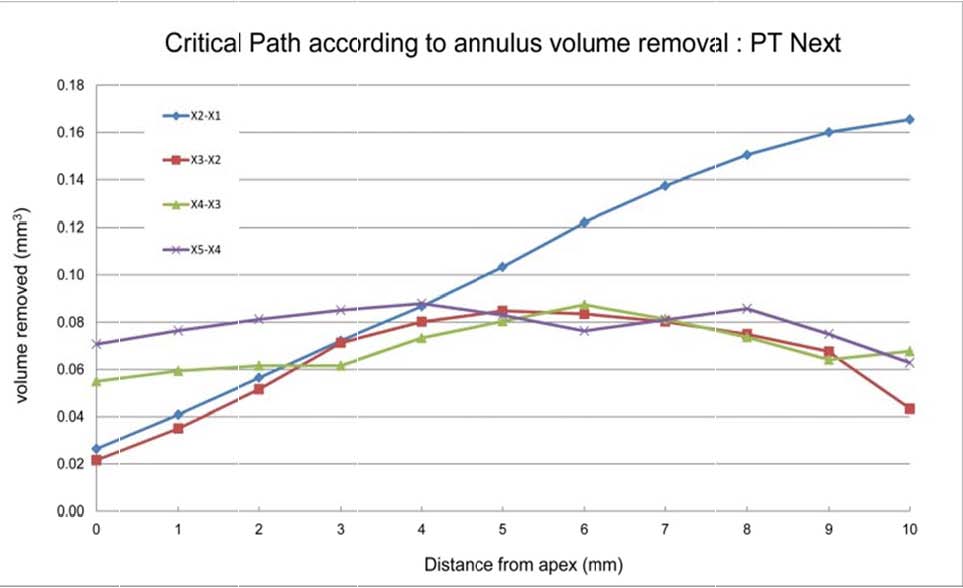
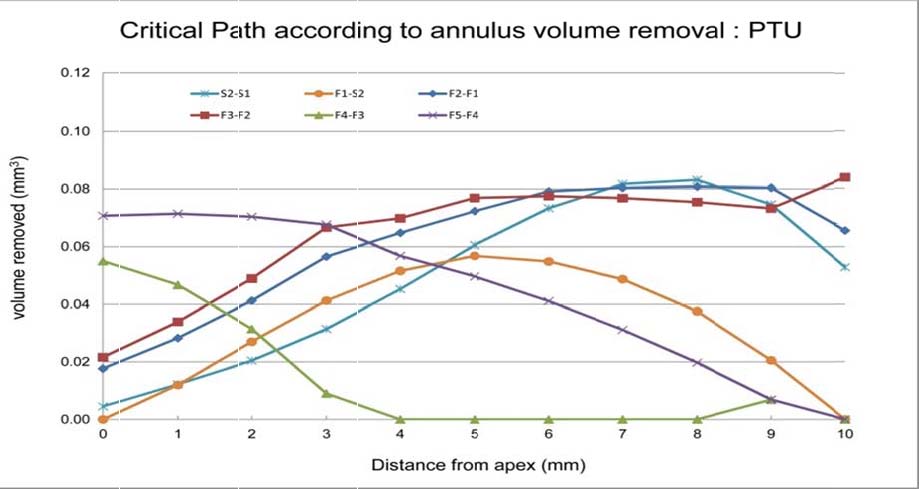
When the same calibrations and calculations are made for the predecessor the ProTaper Next, namely, ProTaper Universal, in which the ISO system of file sequencing was utilized, a disparity in volumetric removal is noted (figure 7).
Further testing was undertaken to demonstrate that this improvement in file design assists in endodontic cavity preparation in minimization of transportation, which is part of the next discussion, Instruments of Critical Path – Dynamics of Precession -Mechanical Analysis.
Conclusions
References
Abou Ross M, Frank, AL and Glick DH: The anti-curvature method to prepare the curved root canal. J Am Dent Assoc. 101:792, 1980
Arpaio, J. An endodontic instrument. U.S. Patent No. 4,538,989, Sept, 1985.
Calberson, FL, Deroose, AJ, Hommez, GM, and DeMoor, RJ: Shaping ability of GT Rotary Files in simulated resin root canals. Int J Endod 35:607-614, 2002
Coffae EP, Brilliant ID: The effect of serial preparation on tissue removal in the root canals of extracted mandibular human molars. J. Endod, 6:815-22, 1976
Esposito, PT and Cunningham, CJ: a comparison of canal preparations with nickel-titanium and stainless steel instruments. J Endod 21:173-176, 1995
Glosson, CR, Haller, RH, Dove, SB, and Del Rio, CE: A comparison of root canal preparations using N-Ti hand, Ni-Ti engine-driven and K-flex endodontic instruments. J Endod, 21:146-151
Heath, DE. Endodontic instrument. U.S. Patent No. 4,871,312, Oct, 1989
Hess, W and Zurcher, E: The anatomy of the root canals of the teeth of the permanent dentition and the anatomy of the root canals of the teeth of the deciduous dentition and of first permanent molars. William Wood & Co., New York, 1916
Hulsman, M, and Stryga, F: Comparison of root canal preparations using different automated devices and hand instrumentation. J Endod 19:141-145, 1993
Hunter, W: The role of sepsis and antisepsis in medicine. Lancet, Jan, 79, 1911
Gambarini, G: Cyclic fatigue of Profile rotary instruments after prolonged clinical use. Int Endo J, 34:386-389, 2001
Johnson, WB: Method of endodontic preparation of a root canal and a file set for use in the method, USPTO 6106296, August 2000
Kerr, MM. Dental Instrument, USPTO No. 1,307,446, June, 1919
Kum, KY, Spängberg, L, Bruce, YC, Jung, IY, Seung-Jong, L and Chan-Young, L. Shaping ability of three Profile rotary instrumentation techniques in simulated resin root canals. J. Endod 26:719-723, 2000
Maynard, E (Washington, D.C.): First root canal instrument. History of Endodontics, Ingle’s Endodontics, 6th edition, 2009
McSpadden, JT: Endodontic instrument. U.S. Patent No. 4,457,710, July, 1984
McSpadden, JT: Endodontic instrument. U.S. Patent No. 5,735,689, April,1998
Maillefer, PL and Aeby, F: Instrument for boring dental radicular canals. US Patent No. 5,746,597, May, 1998
Mandel, E, Machtou, P, Friedman S: Scanning electron microscope observation of canal cleanliness. J Endod, 16:279-83, 1990
Marshall, Fl and Pappin, I: A crown-down pressure less preparation root canal enlargement technique. Technique manual. Portland, Ore, Oregon Health Sciences University, 1980
Roane IS and Sabala CL, and Duncanson MG Jr: The “balanced force” concept for instrumentation of curved canals. I Endod 11:203, 1985
Rosenow, EC: The relationship of dental infection to systemic disease. D Cosmos 59:485- 491, 1917
Schäfer, E: Relationship between design features of endodontic instruments and their properties. Part 2. Instrumentation of curved canals. J Endod 25:56-59, 1999
Schäfer, E. and Florek, H, Efficiency of rotary Nickel-titanium K3 instruments compared with stainless steel hand K-Flexofile. Part 1. Shaping ability in simulated curved canals. Int Endo J 36:199-207, 2003
Schilder H: Cleaning and shaping the root canal. Dent Clin North Am 18:269, 1974
Schilder, H: Set of endodontic instruments. U.S. Patent. No. 5,017,138, May, 1991
Stewart, CC: The importance of chemomechanical preparation of the root canal. Oral Surg 8:993-997, 1955
Walia, H, Brantley, WA, and Gerstein, H: An initial investigation of the bending and torsional properties of nitinol root canal files. J Endod, 14:346-351, 1988
Weine FS, Kelly RF, and Lio PI: The effect of preparation procedures on original canal shape and on apical formation shape. J Endod 1:255, 1975
Publication pending. All rights are reserved by Critical Path Technology. The contents of this article may not be reproduced, downloaded, disseminated, published, or transferred in any form or by any means, except with the prior written permission.